中文笔记：Haptic interaction based SPH fluid control

基于触觉交互的SPH流体控制

记录读的一篇CASA 2017的文章，这个Haptic就暂时翻译成触觉了，大概那个意思。

文章有些让人迷惑的地方，引用文献有问题、还有公式和以往的论文有些不对应。总体无伤大雅，主要看看这个新想法。

摘要

• 流体控制已成为近年来的研究热点。
• 提出了一种基于触觉相互作用的SPH流体变形控制方法。
  • 首先，利用体素化方法对用户指定的对象模型进行采样，得到控制模型和控制流体的动画。
  • 然后，为了实现逼真的交互效果，我们根据用户控制力以及模型与流体之间的交互力来计算控制模型的变形。
  • 最后，提出了一种流体模型变形控制方法。

介绍

• 触觉相互作用的流体控制是一门开放的、主动的学科。

• 传统的方法只提供简单的触觉交互作用。

• 相关工作

  • Terzopoulos等率先提出了基于物理的触觉相互作用计算方法。
  • Mora采用基于网格的方法模拟了流体与固体的相互作用，并通过求解Navier-Stokes方程计算了流体力的反馈力。
  • Yang等模拟了固体和气体之间的触觉相互作用。该方法遵循流体动力学的基本规律，通过测量周围网格的信息生成三维纹理。
  • Cirio等采用SPH方法模拟了流体与固体之间的相互作用。该方法利用SPH框架对固体和液体进行建模，通过力反馈装置控制反馈力的输入，并通过力反馈装置实现触觉交互仿真。
  • Wang等采用混合方法模拟流固相互作用，其中固体在网格中模拟，流体采用传统的SPH方法计算。
    用该方法计算的相互作用力光滑、真实。但是，它的计算成本仍然很高。

• 本文提出了一种基于触觉相互作用的SPH流体变形控制新方法。
• 在触觉交互过程中，用户通过触觉交互装置将力输入到虚拟场景中，并用控制力控制模型的变形，从而驱动流体模型变形。

在交互过程中，为了使流体模型的变形更加自然考虑了外部流体压力、浮力和粘滞力。

• 主要贡献

  1. 提出了一种基于触觉交互作用的SPH流体控制方法，该方法可以提供流体模型的变形约束，有效地控制流体模型的变形。
  2. 提出了一种基于交互作用的控制模型变形方法，用于计算应用交互力时控制模型的变形，为用户提供更丰富的交互体验。
  3. 采用了一种流体变形约束控制方法，可以保证流体质点随控制模型的变形而自然变形。

算法

SPH流体控制通过触觉相互作用

对于每个粒子，使用以下方法来计算流体的相互作用力。

变形固体粒子的力的图解

$f_{interaction} = f_{bouyancy}+f_{pressure}+f_{viscosity} \tag 1$

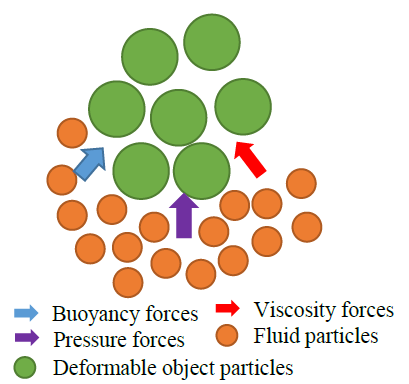
其中$f_{interaction}$是触控力，$f_{pressure}$是压力，$f_{viscosity}$是粘滞力。为了尽可能地提高真实性，在相互作用力中引入浮力$ f_{bouyancy}$。粒子所受压力的计算方法如下:

$f_{\text {pressure}}(i)=-\sum_{j \in N(i)} \frac{P_{j}+P_{i}}{2} \nabla W\left(p_{i}-p_{j}, \mathrm{H}\right) \tag 2$

式中，$j∈N(i)$为粒子$i$邻域内的粒子，$P_j$和$P_i$代表粒子$j$和粒子$i$， $p_i$和$p_j$是粒子的位置。

$\rho_{i}=\sum_{j \in N(i)} m_{i} W\left(p_{i}-p_{j}, \mathrm{H}\right) \tag 3$

$m_i$是附近粒子$i$的质量。此外，粘滞力也是不可或缺的，可计算为

$f_{v i s c o s i t y}(i)=\mu \cdot m_{i} \cdot \Delta t\left(\Delta u_{i}-u_{i}\right) \tag 4$

其中$μ$是粘度系数,$m$是质量,$u$是速度,我$Δu_i$计算如下：

$\Delta u_{i}=\frac{\sum_{j \in N(i)} u_{i} W\left(p_{i}-p_{j}, \mathrm{H}\right)}{\sum_{j \in N(i)} W\left(p_{i}-p_{j}, \mathrm{H}\right)} \tag 5$

最后，由于控制模型在流体中不同位置的浮力是不同的，流体浮力相互作用的计算采用统一的SPH流体建模框架。根据浮力的物理性质，浮力与重力方向相反，表示为

$f_{\text {bouyancy}}(i)=-\sum_{j \in N(i)} \rho_{j} d_{j} W\left(p_{i}-p_{j}, \mathrm{H}\right) \tag 6$

通过以上计算过程，可以得到控制模型与流体相互作用过程的总相互作用力$f_{interaction}$。
则t时刻对模型变形的外力之和表示为：

$f_{e x t}^{t}(i)=f_{\text {interaction}}^{t}(i)+f_{\text {haptic}}^{t}(i)+G \tag 7$

流体模型变形的约束控制

本文针对控制模型中粒子堆积的控制问题，提出了以下策略，以提高流体颗粒的充填能力。

• 首先计算了流体的密度，得到了控制区域的密度场。

• 当流体颗粒填充在较好的区域时，密度场越大，反之亦然。

• 引入了一种新的比例因子，在该比例因子的作用下，可以根据周围流体颗粒的密度将控制力缩放到一定的比例。

  $f_{a}(j)=w_{a} \sum_{i} \beta_{i} \frac{p_{i}-p_{j}}{\left\|p_{i}-p_{j}\right\|} W\left(x_{i j}, H\right) \tag 8$

  $\beta_{i}=1+\frac{\rho_{0}}{\left(\rho_{i}+\eta\right)} \tag 9$

$\rho_0$是流体颗粒的初始密度，$\eta$是non-zero比例因子，$m_j$是流体粒子的质量，$\rho_i$是第$i$个控制粒子的密度。$\beta_i$为第$i$个控制粒子的比例因子。

另一方面，源控颗粒子在运动过程中，存在粒子运动过快导致流体粒子突然失去控制的问题，从而造成流体粒子的非自然飞溅问题。为了解决这一问题，本文采用弹簧结合力来控制快速运动条件下的流体颗粒飞溅问题。

本文以流体粒子与被控粒子之间的距离为关键参数，寻找最接近当前流体粒子的控制粒子。
当流体颗粒远离控制颗粒时，控制颗粒将对其施加一个拉力，使其返回到控制范围。
当流体颗粒与控制颗粒太接近时，控制颗粒会产生推力。
弹簧约束公式如下：

$f(d)=\frac{1}{1+e^{\gamma-\delta \mathrm{D}}} \tag {10}$

式中，D为流体粒子到控制粒子的距离，$\gamma$和$\delta$为调节弹簧力函数的可变参数。综上所述，将弹簧约束应用于控制力，得到如下公式:

$f_{\text {spring}}(i)=\tau f\left(\left|r_{i}-p_{i}\right|\right) \frac{r_{i}-p_{i}}{\left|r_{i}-p_{i}\right|} \tag {11}$

其中，$\tau$调整弹簧的强度，$r_i$是第一个流体粒子的位置，$p_i$是距离控制粒子最近的粒子的位置。

ps：在基于位置地流体控制中，$r_i$是最近控制粒子位置，$p_i$是流体粒子位置，该文章又些许差异

实验及结果

Cirio等人的方法(a)与本文方法(b)变形效果比较

图3显示了本文方法与Cirio等人方法的对比。可以看到，由于本文方法涉及浮力，控制模型的交互过程更加真实和自然。

ps：emmm…

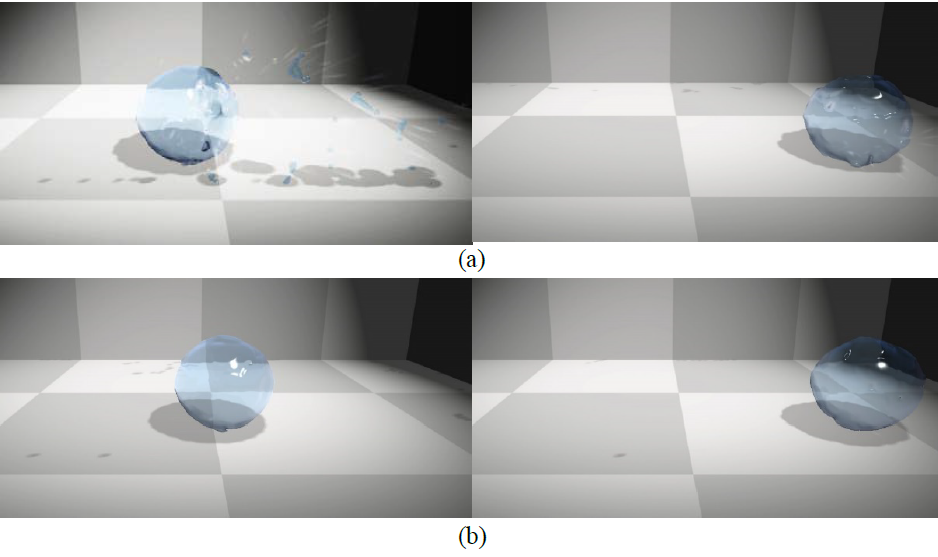
Solenthaler等人方法与本方法对照效果比较。(a)为原粗糙控制方法；(b)是流体模型变形约束控制方法。

对于流体模型控制，传统的方法Solenthaler只提供了一个粗糙的控制力，不适用于可变形的流体触觉交互作用场景。
(a)是传统控制方法的结果，只考虑了粒子对流体粒子引力的控制。
(b)是本文结果，其中不仅考虑了控制颗粒对流体颗粒的粗控制约束，还引入了弹簧力约束和速度约束。
通过对比图(a)和图 (b)可以看出，当变形较大时，(a)控制模型中存在明显的粒子飞溅，而(b)控制模型可以很大程度上保持流体模型的形状。

结论

• 提出了一种基于触觉相互作用的SPH流体变形控制方法。
• 提出了一种基于交互控制模型的变形控制算法来计算控制模型的变形。
• 此外，还设计了一种流体变形控制方法，以有效地控制流体模型。