1. 论文（Position-Based Fluid Control）

概述
- 一种新的流体动力学控制方法，该方法能够驱动基于粒子的流体模拟，以匹配快速变化的目标，同时保持自然的类流体运动。
- 首先通过采样目标形状来生成控制粒子，然后对每个控制粒子应用非线性约束，使其相邻的流体粒子在其影响区域内保持恒定的流体密度。
- 这种密度约束高度符合流体的不可压缩性质；可以驱动流体以自然的方式匹配目标形状。
- 为了匹配快速移动或变形的目标，为控制区域中的每个流体粒子添加了一个自适应弹簧，连接到其最近的控制粒子。只有当流体颗粒远离其对应的控制颗粒时，弹簧约束才会生效，以避免引入人为粘度。因此，即使目标形状迅速变化，流体粒子也能得到很好的控制。
- 此外整合速度约束来调整被控流体的刚度。所有这三个约束条件在基于位置的框架下得到解决。

相关工作总结笔记
算法

第一部分是生成控制粒子。它包括两个主要阶段:1)将模型采样到粒子表示中;2)利用骨骼运动数据对采样的粒子进行变形。注意，这部分是在模拟loop之前执行的，生成的控制粒子被用作控制求解器的输入

方法的核心是一个基于位置的控制求解器，它包含三个不同的约束:密度约束、弹簧约束和速度约束。

密度约束用于驱动流体匹配目标形状，同时保留流体运动的细节。当目标快速移动时，使用弹簧约束将流体拉回控制域。速度约束能够控制流体的速度，使流体紧紧跟随目标物。
- 生成控制粒子
  
  该部分未重点实现
  
  这部分涉及到两种算法:采样算法和骨架驱动变形算法。该采样算法用于对由动画师提供的目标模型进行采样，以生成相应的控制粒子。骨架驱动变形算法在生成的控制粒子集上工作，它允许动画师标记关节，然后驱动粒子集变形基于骨骼运动数据。
  
  为了对网格模型进行采样，首先遵循现有的体素化方法[Dionne和de Lasa 2013]。然而，结果是原始模型的锯齿状表示，特别是在采样分辨率较低的情况下，如图2(顶部)所示。导致结果不佳的关键原因是生成的控制粒子的位置固定在其对应体素细胞的中心。发现对基本的体素化算法进行细微的修改可以避开这个问题。首先执行一个朴素的网格细分过程，即将一个网格三角形分割为两个，如果它的边长大于体素单元的大小，如图3所示。分割后，将位于体素细胞内的顶点作为其对应控制粒子的位置，而不是体素细胞的中心。如果多个顶点落在同一个体素单元格中，只需对这些位置进行平均。最后，使用种子填充算法对模型的内部实体进行体素化。网格模型的细化粒子表示如图2(底部)所示。
  
  图3:朴素三角形划分: $\Delta V_1V_2V_3$ 被划分为 $\Delta V_1V'V_3$ 和 $\Delta V'V_2V_3$ ，其中 $V'$ 为 $V_1V_2$ 的中心
  
  的采样方法比传统的体素化技术产生更平滑的表示。虽然的方法不能保证生成的控制粒子在模型表面的均匀分布。后续的控制求解器对控制粒子的分布没有严格要求。
  
  为了用骨骼运动数据变形生成的控制粒子，首先需要动画器标记每个关节的位置。然后计算每个骨骼影响的每个体素的权重[Dionne和de Lasa 2013]:首先使用吉布提算法计算体素 $j$ 与其对应的骨骼 $i$ 之间的最短距离 $d^i_j$ ;那么骨 $i$ 权重对体素细胞 $j$ 的影响 $w^i_j$ 为:
  
  $w_{j}^{i}=\left(\frac{1}{(1-\alpha)\left(d_{j}^{i}\right)+\alpha\left(d_{j}^{i}\right)^{2}}\right)^{2} \tag 1$
  
  其中 $\alpha$ 是允许动画师控制绑定平滑度的参数，在的实验中为0.3。最后，对权重进行归一化步骤:
  
  $\tilde{w}_{j}^{i}=\frac{w_{j}^{i}}{\sum_{k} w_{j}^{k}} \tag 2$
  
  应用骨架运动后的平滑字符变形如图4所示。
  
  图4:3.1节中采样和变形算法输出的图例:原始网格模型(左上)，采样结果(右上)，不同颜色加权结果(底部)，平滑骨架驱动变形结果(右下)
- 密度约束
  
  生成的控制颗粒实际上指定了模拟空间中流体的靶分布。为了使流体与目标形状相匹配，最直接的方法是使用恒定的引力将流体颗粒拉向控制颗粒。但是，这种朴素的方法会导致流体颗粒在控制颗粒中心出现聚类和聚集现象，导致控制区域的密度高于自由状态流体。为了解决这个问题，Th¨urey et al.根据控制粒子的密度减小了引力[Th¨urey et al. 2009]。然而，硬约束很难使用基于强制的方法来定义。
  
  与基于引力的方法不同，采用了符合流体不可压缩特性的密度约束。
  
  控制粒子把它自己和它的邻近流体粒子当作一个系统，并设法通过移动它的邻近流体粒子来达到一个恒定的密度，如图5所示。
  
  的想法是受到PBF [Macklin and Miller 2013]的启发，PBF解决了每个流体粒子与其相邻粒子的密度约束，以加强不可压缩性。与他们的工作不同的是，在模拟中引入了控制粒子，并对每个控制粒子与其相邻流体施加密度约束粒子。
  
  本文将 $i_{th}$ 控制粒子表示为其位置 $P_i$ ，将 $i_{th}$ 流体粒子表示为其位置 $p_i$ ，对第 $i$ 个控制粒子的大小约束表示为:
  
  $C_{i}\left(P_{i}, p_{1}, \cdots, p_{n}\right)=\frac{\tilde{\rho}_{i}}{\tilde{\rho}_{0}}-1 \tag 3$
  
  $\tilde{\rho}_{i}=\sum_{j} m_{j} W\left(P_{i}-p_{j}, H\right) \tag 4$
  
  式中， $\rho_0$ 为控制粒子的剩余密度， $p$ 为第 $i$ 个控制粒子支持半径内的流体密度。使用标准SPH密度估计器定义 $\tilde{\rho}_{0}$ 。 $m_j$ 为流体粒子 $i$ 的质量，将其作为一个单位值，因此在后面的方程中省略。 $H$ 为控制粒子的支持半径。控制颗粒支持半径越大，控制性能越强。
  
  状态方程(3)给出了每个控制粒子的非线性密度约束。因此，对于每个流体颗粒，需要一个以 $\Delta p_i$ 表示的位移，使式(3)满足:
  
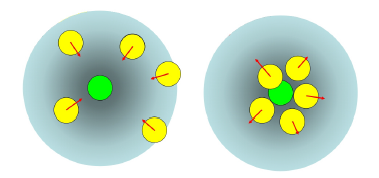
  $C_{i}\left(P_{i}, p_{1}+\Delta p_{1}, \cdots, p_{n}+\Delta p_{n}\right)=0 \tag 5$
  
  图5:这个图说明了对控制粒子的密度约束(绿色)。在其支持半径(灰色)中，当流体密度小于其静止密度时，流体颗粒(黄色)将被吸引到控制颗粒(左边);否则，流体颗粒将被排斥从中心(右)。
  
  采用基于位置的动态方法|Miller et al. 2007]来求解这个非线性方程。根据PBD, $\Delta p$ 沿着约束的导数方向，其估计为:
  
  $\Delta p_{j}=\tilde{\lambda}_{i} \nabla_{p_{j}} C_{i}\left(P_{i}, p_{1}, \ldots, p_{n}\right)$
  
  其中 $\tilde{\lambda}_{i}$ 为约束 $i$ 的标量值，每个约束 $i$ 对该约束下的所有流体粒子具有相同的， $\tilde{\lambda}_{i}$ 由一下给出：
  
  $\tilde{\lambda}_{i}=-\frac{C_{i}\left(P_{i}, p_{1}, \ldots, p_{n}\right)}{\sum_{j}\left|\nabla_{p_{j}} C_{i}\left(P_{i}, p_{1}, \ldots, p_{n}\right)\right|^{2}+\varepsilon} \tag 7$
  
  其中 $\varepsilon$ 是一个软化系数，避免了除以一个非常小的值而使模拟不稳定。第 $j$ 个流体粒子的约束 $C_i$ 推导为[Monaghan 1992]:
  
  $\nabla_{p_{j}} C_{i}=-\frac{1}{\tilde{\rho_{0}}} \nabla_{p_{j}} W\left(P_{i}-p_{j}, H\right) \tag 8$
  
  最后，将控制颗粒对流体颗粒施加的所有位移相加，得到密度约束:
  
  $\Delta p_{i}^{\text {density}}=-\alpha \frac{1}{\tilde{\rho_{0}}} \sum_{j} \tilde{\lambda}_{j} \nabla_{p_{j}} W\left(P_{j}-p_{i}, H\right) \tag 9$
  
  在这里，为每个控制粒子合并从0到1的 $\alpha$ 来表示密度约束的强度。
- 弹簧约束
  
  流体模拟控制是一项具有挑战性的任务。简单地设置强约束来解决这一问题，会产生明显的人工粘度。作为一个结果。被控制的流体将看起来像一个刚体和失去丰富的流体细节。
  
  与基于网格的流体模拟框架相比，基于颗粒的控制方法更难解决这一问题。原因是粒子的支撑半径长度是有限的。
  
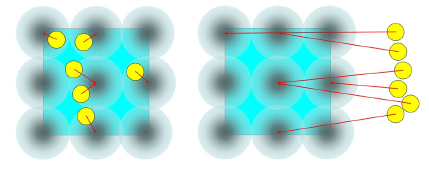
  图6:该图说明了如何使用弹簧约束来处理快速移动的目标。当流体粒子(黄色)在控制域(浅蓝色)内时，它们分别找到一个参考控制粒子。右:一旦流体粒子远离控制域，弹簧约束(红色箭头)将帮助把它们拉回来。还发现基于SPH公式的其他约束不能工作，因为控制粒子的影响区域无法到达它们。
  
  一旦目标在某些帧中移出半径。控制颗粒的约束对流体颗粒没有影响，这使得流体颗粒失去控制(图6)。
  
  在此，提出了一种适用于基于颗粒的流体模拟框架的新方法，以回避这个长期存在的问题。在流体粒子和它最近的控制粒子之间添加一个自适应弹簧约束，称之为参考。当流体粒子远离它的参考点时，弹簧约束将把流体粒子拉回它的参考点。否则，弹簧约束对流体颗粒的影响很小，因此不会引入人工粘度等副作用。
  
  为了构造一个满足上述特征的弹簧，使用下面的算法来添加和更新每个流体粒子的弹簧。
  
  其中， $d$ 表示控制粒子的最大采样间隔，等于实验的支持半径。当流体粒子处于控制区域时，它会不断更新其参考，其弹簧长度始终小于 $d$ 的一半。将弹簧约束强度定义为:
  
  $f(x)=\frac{1}{1+e^{b-a x}} \tag {10}$
  
  这个公式在机器学习中被广泛用作logistic回归函数。使用这个函数是因为它具有上界和下界的优势(图7)。此外，通过调整两个参数 $a$ 和 $b$ ，可以轻松地使弹簧约束对控制区域内的流体粒子影响很小或没有影响。一旦流体粒子远离控制区域，它们将无法找到最近的控制粒子，因此不会更新它们的引用。在这种情况下，弹簧约束将产生显著的效果，并立即将流体粒子拉回控制区域。对于 $f$ 的上界，的弹簧约束强度不会无限增长，从而避免造成仿真的不稳定。
  
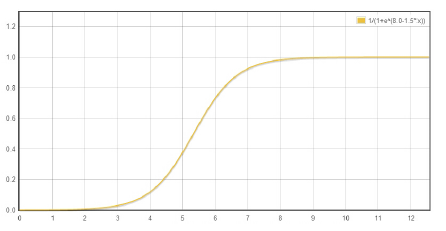
  图7:函数 $f$ 表示与弹簧长度相关的弹簧约束强度。 $f$ 中的参数 $b$ 表示达到最大值前的剩余长度， $a$ 表示梯度。这里，选择 $b$ 是8.0 $a$ 是1.5。
  
  此外，为每个弹簧约束定义了生命周期，每个框架都有一点时间流逝。基于这一特性，可以实现液滴等视觉效果，因为弹簧约束不会永远存在，部分流体粒子会摆脱控制。在的实验中，将生命时间设置为一个固定范围内的随机值。
  
  总之，这个简单但专用的弹簧约束允许控制流体模拟，以跟踪快速变化的目标，同时保持丰富的视觉细节。图8通过一个2D示例演示了弹簧约束的强度。
  
  图8:这个图说明了与控制粒子位置(绿色)相关的弹簧约束的强度和方向。白色表示弹簧强度信息，控制粒子附近区域弹簧约束很少或没有约束。只有当流体粒子远离控制粒子时，弹簧约束才会起作用。此外，弹簧约束不会无限增大。
  
  最后给出了弹簧约束的位移:
  
  $\Delta p_{i}^{\text {spring}}=\beta f\left(\left|r_{i}-p_{i}\right|\right) \frac{\left(r_{i}-p_{i}\right)}{\left|r_{i}-p_{i}\right|} \tag {11}$
  
  其中， $\beta$ 是用于调整弹簧约束强度的参数。 $r_i$ 表示流体粒子i的参考，当然，如果流体粒子没有参考，则不应用弹簧约束。
- 速度约束
  
  速度约束用来改变流体的流动。在某些场景中，动画师可能希望控制流体沿着指定的路径流动，或者模拟一种僵硬的流体。在这种情况下，上述两个约束是不够的。速度约束用来修改整个流动是必要的。它可以驱动流体粒子紧随着目标形状的运动。
  
  对于每个流体粒子，插值其附近控制粒子施加的速度约束。
  
  $\Delta v_{i}=\frac{\sum_{j} V_{j} W\left(p_{i}-P_{j}, H\right)}{\sum_{j} W\left(p_{i}-P_{j}, H\right)} \tag {12}$
  
  $V_j$ 为第 $j$ 个控制粒子的速度， $v_i$ 是流体粒子的速度。则速度约束位移为:
  
  $\Delta p_{i}^{\text {velocity}}=\gamma \Delta t\left(\Delta v_{i}-v_{i}\right) \tag {13}$
  
  式中 $\gamma$ 为速度约束强度。
  
  如前所述，与方法最相关的工作[Thurey et al. 20091]主要使用这种速度约束来控制总体流量。避免压制小尺度的流体细节。他们只在流体速度的低频部分应用这个约束。
  
  在的方法中，速度约束通常只是辅助使用，除非希望产生一个刚性流体模型，否则定义速度约束不会太困难。因此，简单地对整个速度场施加速度约束，而省略了速度分解步骤。

2.实现

简述

将控制求解器集成到PBF流体仿真框架中。算法2对仿真回路进行了概述。除了从第8行到第21行集成控制求解器之外，其他部分与原始PBF相同。与大多数基于粒子的流体模拟一样，主要的计算时间花在寻找邻近的粒子上。每个控制粒子需要找到它的邻近的流体粒子来计算它的密度，每个流体粒子也需要找到它的邻近的控制粒子来累积控制位移。只有当控制粒子有运动时，我们需要重新计算流体粒子的控制粒子邻居。
使用开源库SPlisHSPlasH

SPlisHSPlasH is an open-source library for the physically-based simulation of fluids. The simulation in this library is based on the Smoothed Particle Hydrodynamics (SPH) method which is a popular meshless Lagrangian approach to simulate complex fluid effects. The SPH formalism allows an efficient computation of a certain quantity of a fluid particle by considering only a finite set of neighboring particles. One of the most important research topics in the field of SPH methods is the simulation of incompressible fluids. SPlisHSPlasH implements current state-of-the-art pressure solvers (WCSPH, PCISPH, PBF, IISPH, DFSPH, PF) to simulate incompressibility. Moreover, the library provides different methods to simulate viscosity, surface tension and vorticity.

The library uses the following external libraries: Eigen, json, partio, zlib, cxxopts, tinyexpr, toojpeg, pybind, glfw, and imgui or AntTweakBar. All external dependencies are included.

Furthermore we use our own libraries:
- PositionBasedDynamics to simulate dynamic rigid bodies
- Discregrid to detect collisions between rigid bodies
- CompactNSearch to perform the neighborhood search
- cuNSearch to perform the neighborhood search on the GPU
- GenericParameters to handle generic parameters
SPlisHSPlasH can export the particle data in the partio and vtk format. If you want to import partio files in Maya, try out our Maya plugin:
- MayaPartioTools
实现效果

github地址Evan-ZJ/PBF-Control: based SPlisHSPlasH (github.com)

有很多细节参数无法复制原文，中间参数有自修改，效果示意：

渲染视频