光滑粒子流体动力学流体中物体背后湍流细节的真实稳定模拟
光滑粒子流体动力学流体中物体背后湍流细节的真实稳定模拟
本文提出了一种新颖的,稳定的湍流合成方法,以模拟在光滑粒子流体动力学(SPH)流体中物体背后产生的湍流细节。首先,通过近似SPH流体中飞行过程中的边界层理论,我们提出了一种涡旋产生模型,以识别哪些流体颗粒从物体表面脱落,以及哪些作为涡流颗粒播种。然后,我们采用Biot-Savart定律的SPH式求和内插公式来计算产生的涡度场的波动速度。最后,结合隐式涡度扩散技术和人工耗散项,实现了涡度场的稳定演化。此外,为了有效地捕获湍流细节以进行渲染,我们针对基于粒子的流体提出了一种基于八叉树的自适应曲面重构方法。实验结果表明,我们的湍流合成方法为模拟SPH流体中障碍物引起的湍流细节提供了一种有效的方法,并且可以轻松地添加到现有的基于粒子的流固耦合管道中。
贡献
我们提出了一种基于颗粒的流体的湍流合成方法,该方法模拟了在运动物体后面产生的逼真的湍流细节,并解决了涡旋场的稳定演化。
我们提出了一种使用MC的基于粒子的流体的有效表面重构方法,该方法仅在围绕流体表面的窄带中构建基于八叉树的自适应距离场。
Overview
我们的湍流综合模型用于模拟SPH流体中运动物体背后的湍流细节。 首先,涡度产生模块通过近似SPH流体中的边界层理论来识别哪些流体颗粒从物体表面脱落,哪些流体颗粒作为VP播种。 其次,脉动速度计算模块使用类似于SPH的Biot-Savart定律的总插值公式来计算源自产生的涡度场的脉动速度。 最后,通过隐式涡度扩散技术和人工涡度耗散项的组合解决了涡度场的稳定演化。
湍流综合方法
涡流产生
与流体耦合的固体是明显的湍流发生器。 计算流体动力学的边界层理论描述了物体的摩擦力在固体边界处强制切向流速为零,这导致形成了流速降低的薄层,称为边界层。 在边界层中,切向流速的弯曲导致形成涡旋薄片。 当边界层在高流动不稳定性区域从固体表面脱落时,涡旋会从边界层喷出,并作为湍流进入流体。 为了模拟固体引起的湍流的物理上合理的形成,如图3所示,我们提出了一种适用于SPH流体的四步涡旋产生模型。
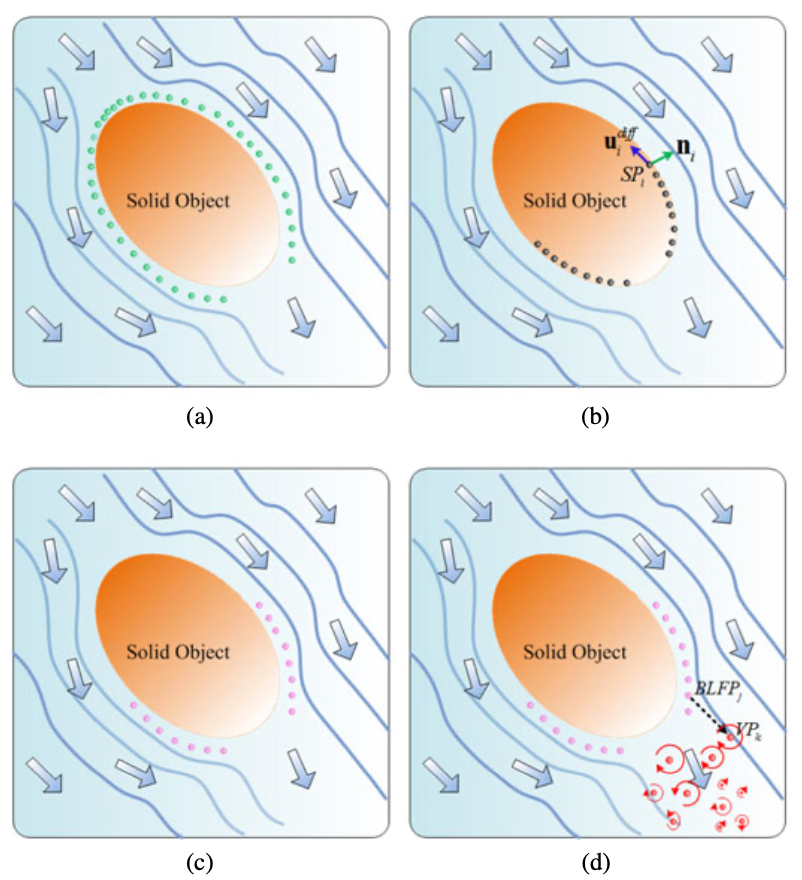
首先,基于边界层理论,我们做出一个近似的假设,即浸没在SPH流体中的物体的边界层由与物体表面的距离小于小阈值的流体粒子组成。我们在本文中设置,因此所有固体表面颗粒的相邻流体颗粒构成了薄边界层。 我们将边界层的每个流体粒子称为BLFP,在图3(a)中将其着色为绿色。
其次,我们确定BLFP从浸没在流体中的物体表面脱落的分离点(SP)。 我们的方法将SP的识别过程分为三个步骤。 首先,我们使用平滑色域的梯度来估计流体-流体界面的法线[38],以计算流体-固体界面的固体颗粒的法线。然后,对每个刚体表面粒子,我们使用计算相对于所有相邻流体粒子的平滑速度差.第三,计算速度差和法线之间的点积。 如果为,则将固体颗粒i标识为SP(图3(b)中为黑色)。
第三,为了模拟浸没在流体中的物体后面的湍流,我们确定了实际上从相邻SP掉落的BLFP。对于一对相邻的粒子BLFP 和SP ,我们计算它们的相对位置与它们的相对速度之间的点积。如果,BLFP 实际上从物体表面脱落(图3(c)中的粉红色)并获得涡度,公式为:
其中是沿物体表面切线方向的相对速度,是用于模拟湍流随机性的随机数,$ \kappa$是控制常数,用于评估流体粘度和物体材料的影响, 是权重因子 。
最后,我们将VP植入SPH流体中。 当携带涡旋的BLFP不再有相邻的固体颗粒时,将其标记为植入流体中的(VP)。 所有VP都构成了由浸没在流体流中的物体引起的涡旋场。 图3(d)表明,通过我们的涡度生成方法,VP最终被植入了物体后面,而不是被随机地植入,它以物理上合理的方式模拟了由固体物体引起的湍流细节。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!